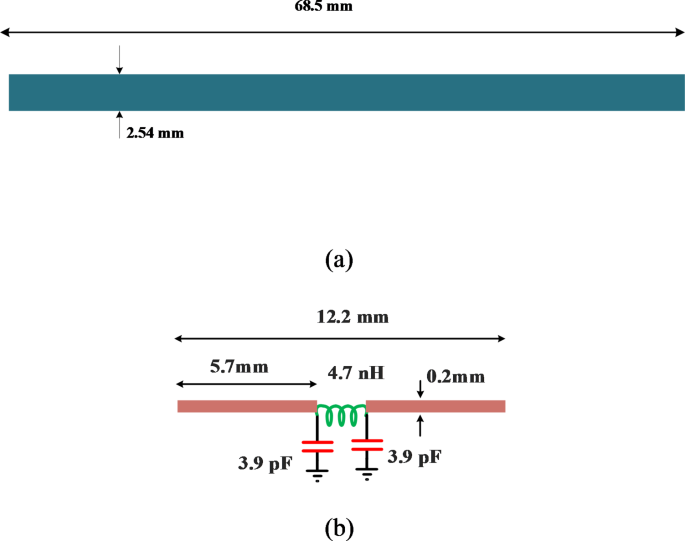
Чтобы оценить эффективность методов уменьшения размеров и подавления гармоник в ответвителях ответвлений, был спроектирован и смоделирован обычный ответвитель на частоте 800 МГц. Как показано на рис. 1, типичный ответвитель состоял из двух вертикальных ветвей сопротивлением 50 Ом шириной 1,56 мм и электрической длиной 90° и двух горизонтальных ветвей сопротивлением 35,4 Ом шириной 2,54 мм и электрической длиной 90°, в результате чего общий размер составлял 0,25 λg × 0,25 λg (68,5 × 68,5 мм). Хотя обычный ответвитель адекватно работал на рабочей частоте, он не смог подавить нежелательные гармоники на более высоких частотах, что привело к ухудшению характеристик.
Принципиальная схема (а) и частотная характеристика (б) обычного QHC 800 МГц. Размеры указаны в мм.
Предлагаемые композитные линии
Размер обычного соединителя был большим из-за четырех длинных ветвей электрической длины по 90°. Для решения этой проблемы в предлагаемой конструкции соединителя используются составные линии. На рисунке 2(а) показана структура предлагаемой горизонтальной составной линии, а на рисунке 2(б) показана типичная горизонтальная линия. На частоте 800 МГц обе линии работают одинаково хорошо, но предлагаемая составная линия эффективно подавляет более высокие частоты и имеет значительно меньшие размеры по сравнению с традиционной конструкцией.
В этом разделе изначально проектируется условная линия и определяется ее матрица ABCD. Впоследствии предлагаемая линия была усовершенствована путем объединения двух микрополосковых линий, двух конденсаторов и одной катушки индуктивности. Крайне важно, чтобы обе линии демонстрировали одинаковую производительность на рабочей частоте 800 МГц. Затем выводится матрица ABCD предложенной линии, которая должна быть равна матрице ABCD обычной линии. Решив полученное уравнение, путем взаимосвязанных расчетов получают значения катушки индуктивности и конденсаторов, а также длину и ширину предполагаемой линии.
Структура (а) обычная длинная горизонтальная линия λg/4 и (б) компактная предлагаемая составная линия.
Для анализа предлагаемой компактной составной линии (CLC), показанной на рис. 2(б), можно использовать матрицу ABCD. Матрица ABCD для сосредоточенных элементов ХЖК представлена в уравнении. (1). Эту матрицу можно рассчитать путем умножения матриц ABCD C, L и C.47.
$${{\text{M}}_{{\text{Сосредоточенные\_Elements}}}}=\left( {\begin{array}{*{20}{c}} {1 — C\,L\ ,{\omega ^2}}&{L\,\omega \,{\text{i}}} \\ {C\omega {\text{i}} — C\,\omega \,\left( { C\,L\,{\omega ^2} — 1} \right)\,{\text{i}}}&{1 — C\,L\,{\omega ^2}} \end{array} } \справа)$$
(1)
$${{\text{M}}_{{\text{proposed\_composite\_line}}}}=\;\left( {\begin{array}{*{20}{c}} { — \cos \left( {{\theta _1}} \right)\,{\alpha _2} — \frac{{\sin \left( {{\theta _1}} \right)\,{\alpha _3}\,{ \text{i}}}}{{{Z_1}}}}&{ — \cos \left( {{\theta _1}} \right)\,{\alpha _3} — {Z_1}\,\sin \ left( {{\theta _1}} \right)\,{\alpha _2}\,{\text{i}}} \\ {\cos \left( {{\theta _1}} \right)\,{ \alpha _1} — \frac{{\sin \left( {{\theta _1}} \right)\,{\alpha _4}\,{\text{i}}}}{{{Z_1}}}} &{ — \cos \left( {{\theta _1}} \right)\,{\alpha _4}+{Z_1}\,\sin \left( {{\theta _1}} \right)\,{\ альфа _1}\,{\text{i}}} \end{array}} \right)$$
(2)
$${\alpha _1}=\cos \left( {{\theta _1}} \right)\,\left( {C\,\omega \,{\text{i}} — C\,\omega \ ,{\alpha _5}\,{\text{i}}} \right) — \frac{{\sin \left( {{\theta _1}} \right)\,{\alpha _5}\,{\ текст{i}}}}{{{Z_1}}}$$
(3)
$${\alpha _2}=\cos \left( {{\theta _1}} \right)\,{\alpha _5} — {Z_1}\,\sin \left( {{\theta _1}} \right )\,\left( {C\,\omega \,{\text{i}} — C\,\omega \,{\alpha _5}\,{\text{i}}} \right)\,{ \text{i}}$$
(4)
$${\alpha _3}={Z_1}\,\sin \left( {{\theta _1}} \right)\,{\alpha _5}\,{\text{i}} — L\,\omega \,\cos \left( {{\theta _1}} \right)\,{\text{i}}$$
(5)
$${\alpha _4}=\cos \left( {{\theta _1}} \right)\,{\alpha _5}+\frac{{L\,\omega \,\sin \left( {{\ theta _1}} \right)}}{{{Z_1}}}$$
(6)
$${\alpha _5}=C\,L\,{\omega ^2} — 1$$
(7)
В уравнении (2), значения Z1 и θ1 – импеданс и электрическая длина двух равных линий передачи, расположенных вблизи обеих сторон сосредоточенных компонентов в предлагаемой составной линии. Наконец, матрица предлагаемой составной линии должна быть приравнена к матрице традиционной линии λ/4, которая определена в уравнении. (4). Фактор к следует считать равным «\(\:\sqrt{2}\)» и «1» для горизонтальных и вертикальных линий соответственно.
$${{\text{M}}_{\lambda {\text{/4}}}}=\;\left( {\begin{array}{*{20}{c}} 0&{\frac{ {{\text{i}}{Z_0}}}{k}} \\ {\frac{{{\text{i}}k}}{{{Z_0}}}}&0 \end{array}} \ верно)$$
(8)
Приравнивая (2) и (8), можно вычислить неизвестные параметры. После упрощения будут получены четыре уравнения, как показано в уравнениях. (9)–(12). Для уравнений не существует решения в замкнутой форме. (9)–(12). Поэтому для упрощения, рассмотрев правильные значения Z1 и θ1 исходя из желаемого уменьшения размера, неизвестные значения индуктивности L и емкости C можно рассчитать численно с использованием уравнений. (9)–(12). Различные расчетные значения L и C в зависимости от различного нормализованного импеданса Z1 для горизонтальных ветвей показаны на рис. 3. Значение 7° рассматривается для θ1 по высокой величине уменьшения размеров конструкции. Следовательно, согласно рис. 3, учитывая значения 136 Ом и 7° для линии передачи в горизонтальных ветвях, значения сосредоточенных элементов 3,3 пФ и 6,9 нГн получаются для значений L и C. В соответствии с практическими ограничениями для значений L и C, значения 3,9 пФ и 4,7 нГн рассматриваются для значений L и C. Таким же образом, учитывая значения 167 Ом и 7,5° для линии передачи в вертикальных ветвях, будут рассчитаны значения сосредоточенных элементов 2,7 пФ и 6,8 нГн.
$${Z_1}\,\left( {L\,{Z_1}\,\sin \left( {2\,{\theta _1}} \right)\,{C^2}\,{\omega ^ 3}+2\,\cos \left( {2\,{\theta _1}} \right)} \right)=\omega \,\left( {2\,C\,\sin \left( {2 \,{\theta _1}} \right)\,{Z_1}^{2}+2\,C\,L\,\omega \,\cos \left( {2\,{\theta _1}} \ right)\,{Z_1}+L\,\sin \left( {2\,{\theta _1}} \right)} \right)$$
(9)
$$L\,C^{2} \,Z_{1} ^{2} \,\omega ^{3} \,\sin \left( {\theta _{1} } \right)^{2} + \,\sin \left( {2\,\theta _{1} } \right)\,Z_{1} + L\,\omega \,\cos \left( {\theta _{1} } \ вправо)^{2} = 2C\,Z_{1}^{2} \omega \,\sin \left( {\theta _{1} } \right)^{2} + C\,L\,\ sin \left( {2\,\theta _{1} } \right)\,Z_{1} \,\omega ^{2} + Z_{0}$$
(10)
$$\begin{aligned} & Z_{1} \,{\text{i}} + Z_{0} \,\sin \left( {\theta _{1} } \right)\,\left( { \cos \left( {\theta _{1} } \right)\,\sigma _{1} + \frac{{L\,\omega \,\sin \left( {\theta _{1} } \ right)}}{{Z_{1} }}} \right)\,{\text{i}} = Z_{0} \,Z_{1} \,\cos \left( {\theta _{1} } \right)\,\left( {\cos \left( {\theta _{1} } \right)\,\left( {C\,\omega \,{\text{i}} — C\, \omega \,\sigma _{1} \,{\text{i}}} \right) — \frac{{\sin \left( {\theta _{1} } \right)\,\sigma _{ 1} \,{\text{i}}}}{{Z_{1} }}} \right) \\ & \sigma _{1} = C{\mkern 1mu} L{\mkern 1mu} \omega ^ {2} — 1 \\ \end{aligned}$$
(11)
$$\cos \left( {{\theta _1}} \right)\,\left( {\cos \left( {{\theta _1}} \right)\,\left( {C\,L\, {\omega ^2} — 1} \right)+\frac{{L\,\omega \,\sin \left( {{\theta _1}} \right)}}{{{Z_1}}}} \ right)={Z_1}\,\sin \left( {{\theta _1}} \right)\,\left( {\cos \left( {{\theta _1}} \right)\,\left( { C\,\omega \,{\text{i}} — C\,\omega \,\left( {C\,L{\omega ^2} — 1} \right)\,{\text{i} }} \right) — \frac{{\sin \left( {{\theta _1}} \right)\,\left( {C\,L\,{\omega ^2} — 1} \right)\ ,{\text{i}}}}{{{Z_1}}}} \right)\,{\text{i}}$$
(12)
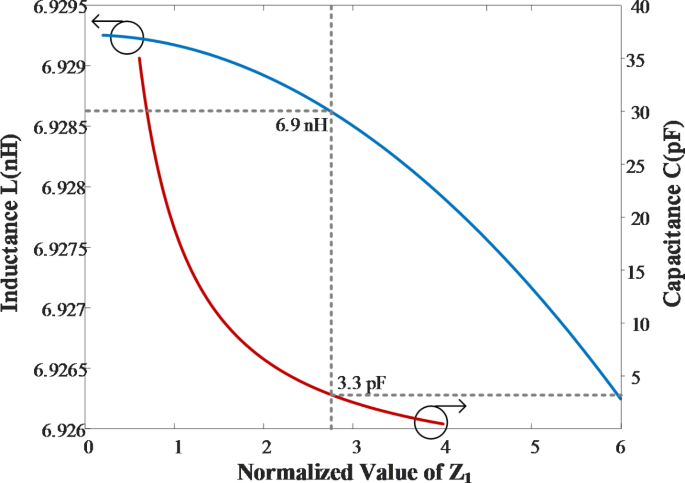
Различные расчетные значения L и C в зависимости от различного нормализованного импеданса Z1 для горизонтальных ветвей. Извлеченные уравнения решаются численно с использованием MATLAB R2021b.
По сравнению с обычной предлагаемая горизонтальная составная линия, состоящая из двух шлейфов диаметром 5,7 мм и сосредоточенного индуктора диаметром 0,8 мм, существенно короче длинной обычной линии длиной 68,5 мм. Такое сокращение длины приводит к уменьшению длины ответвления более чем на 82%, что делает предлагаемый соединитель очень компактным и эффективным. Столь значительное уменьшение габаритов является свидетельством эффективности предложенной конструкции, позволяющей достичь желаемых параметров на рабочей частоте при сохранении как широких полос режекции, так и высокой миниатюризации.
Предлагаемая вертикальная составная линия, показанная на рис. 4(а), и типичная горизонтальная линия, изображенная на рис. 4(b), эффективны на частоте 800 МГц. Однако предлагаемая вертикальная составная линия превосходит по способности подавлять высокие частоты и имеет значительно меньшие размеры по сравнению с традиционной конструкцией.
По сравнению с обычной, предлагаемая вертикальная составная линия, состоящая из двух шлейфов диаметром 6 мм и сосредоточенного индуктора диаметром 0,8 мм, существенно короче длинной обычной линии длиной 68,5 мм. Такое сокращение длины приводит к уменьшению длины ответвления более чем на 81%, что делает предлагаемый соединитель очень компактным и эффективным. Столь значительное уменьшение габаритов является свидетельством эффективности предложенной конструкции, позволяющей достичь желаемых параметров на рабочей частоте при сохранении как широких полос режекции, так и высокой миниатюризации.
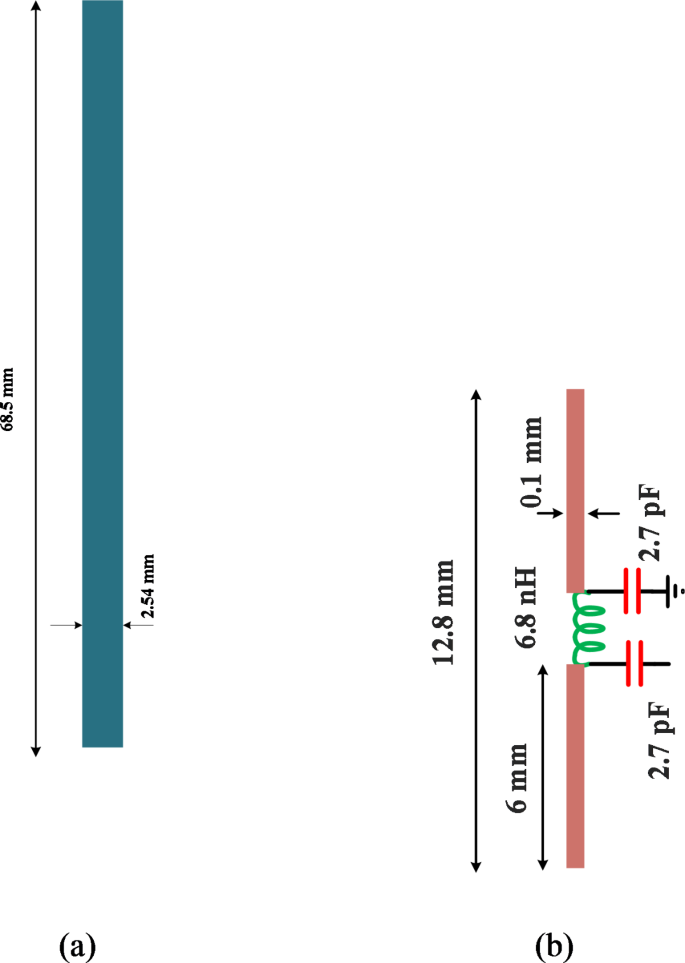
Структура (а) обычная длинная вертикальная линия λg/4 и (б) компактная предлагаемая вертикальная составная линия.
Конфигурация LC-образного фильтра нижних частот, который является основным применяемым блоком для подавления гармоник, изображена на рис. 5 (а), а частотная характеристика этого π-образного фильтра нижних частот изображена на рис. 5 (б). Как показывает частотная характеристика, примененный фильтр имеет частоту среза 1,7 ГГц и обеспечивает полосу задерживания от 3,1 ГГц до более 10 ГГц.
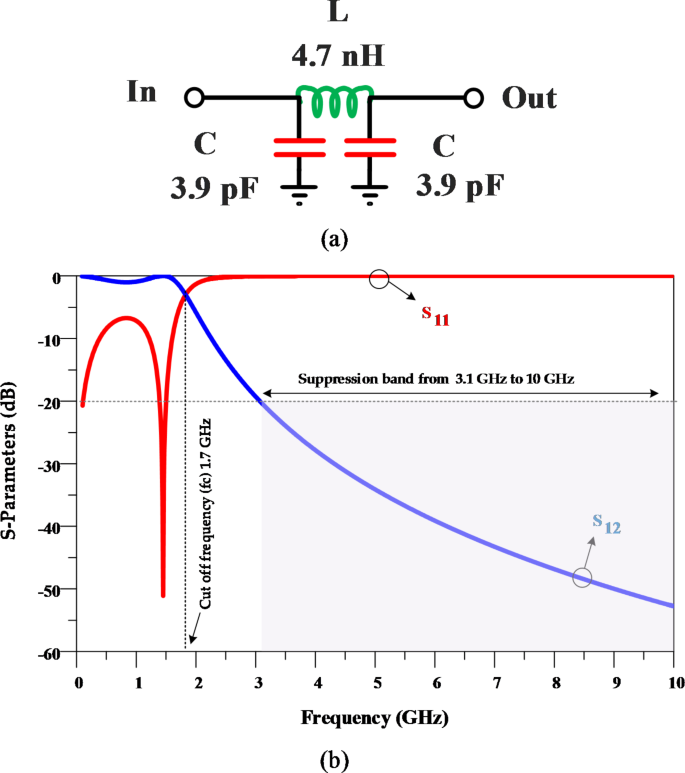
Конфигурация (а) примененный LC π-образный фильтр нижних частот и (б) его частотная характеристика.
ω = 2πf, поэтому частота среза (fС) конфигурации LC π-образного фильтра нижних частот можно получить следующим образом:
$$\:\text{f}\text{c}\:=\frac{1}{2\pi\:\sqrt{\frac{LC}{2}}}$$
(13)
при C = 3,9 PF и L = 4,7 нГн частота среза составляет 1,66 ГГц, что близко к частоте среза, полученной в результате моделирования (1,7 ГГц), что подтверждает процесс проектирования π-образного фильтра нижних частот.




.jpg)










